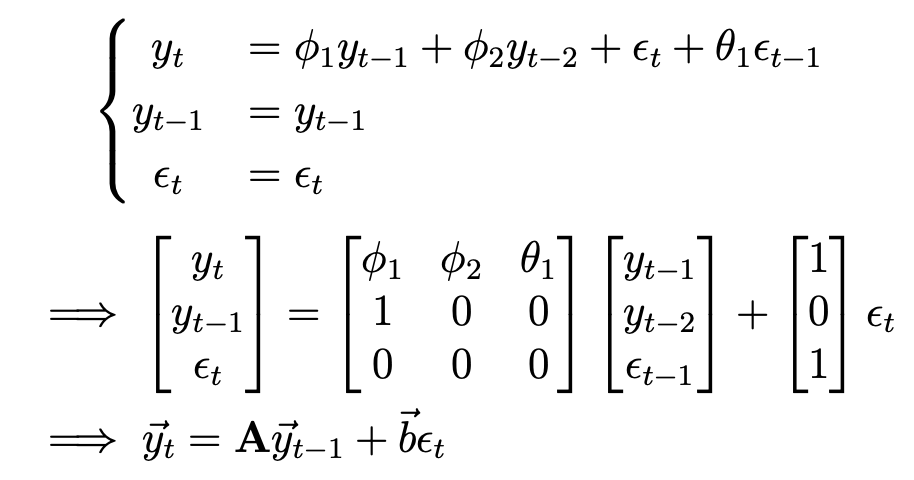Blog

벡터 자기회귀모델은 이전 포스팅에서 다루었던 자기회귀모델의 벡터꼴이다. 예시로 $VAR(1)$을 살펴보자. $$\begin{bmatrix} r_{t} \\ q_{t} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} r_{t-1} \\ q_{t-1} \end{bmatrix} + \begin{bmatrix} \epsilon_{r,t} \\ \epsilon_{q,t} \end{bmatrix}$$ $$ \vec{x_{t}}=\textbf{A} \vec{x_{t-1}}+\vec{\epsilon_{t}}$$ 이전 포스팅에서 $AR(1)=MA(\infty)$로 쓸 수 있던 것처럼 벡터꼴의 자기회귀모델 또한 $VAR(1)$을 $V..

$\underline{Def}$ (Auto-Regressive $p$ Model, AR Model) 자기회귀 p모델 $x_{t}$은 다음과 같이 정의된다. $$x_{t}=\phi_{1}x_{t-1}+\phi_{2}x_{t-2}+\cdots+\phi_{p}x_{t-p}+\epsilon_{t} \;\; where\, \vert \phi \vert < 1$$ 여기서 $\phi$는 모델의 파라미터를, $\epsilon_{t}$는 노이즈를 뜻한다. $\underline{Def}$ (Lag-Operator) 여기서 다음 성질은 갖는 lag-operator $L$을 정의하자. 이는 시계열에서 이전 값을 내놓는 함수다. $(1)$ $L \phi = \phi$ $(2)$ $Lx_{t}=x_{t-1}$ $(3)$ $L^{..

$\underline{Lemma}$ Let $T \colon V \rightarrow W$ be linear & invertible. Then $dim(V) < \infty \Leftrightarrow dim(W) < \infty.$ In this case, $dim(V)=dim(W).$ $\underline{Proof}$ $(\Rightarrow)$ Let $\beta= \{ x_{1}, \cdots, x_{n} \}$ be a basis for $V$. By thm, $T(\beta)$ spans $R(T)=W$. By thm, $dim(W) < \infty$. $(\Leftarrow)$ Since $T^{-1} \colon W \rightarrow V$ is linear & invertible, i..

$\underline{Def}$ Let $T \colon V \rightarrow W$ be linear, where $V,W$ are vector spaces over $\mathbb{F}$. $(i)$ A function $U \colon W \rightarrow V$ is an inverse $T$ if $TU=I_{W},\,UT=I_{V}$. $(ii)$ $T$ is invertible if it has an inverse. $(iii)$ Such an inverse $U$ of $T$ is unique if ie exists. In this case, we write $U=T^{-1}.$ $\underline{Facts}$ Let $T \colon V \rightarrow W,\, U \colo..

$\underline{Def}$ (Left Product Map) Let $A \in M_{m \times n}(\mathbb{F})$. We define a map $L_{A} \colon \mathbb{F}^{n} \rightarrow \mathbb{F}^{m}$ by $$L_{A}(x)=Ax \;\; \forall a \in \mathbb{F}^{n},$$ called the left-product map by $A$. $\underline{Ex}$ $$A = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 2 \end{bmatrix} \in M_{2 \times 3}(\mathbb{R})$$ $$L_{A} \colon \mathbb{R}^{3} \rightarrow \mathbb..

$\underline{Thm}$ $A \in M_{m \times n},\, B \in M_{n \times p}$ Let $$AB=\begin{bmatrix} u_{1} & u_{2} & \cdots & u_{p} \end{bmatrix},\, B=\begin{bmatrix} v_{1} & v_{2} & \cdots & v_{p} \end{bmatrix}$$ Then $$u_{j}=Av_{j}, v_{j}=Be_{j}\;\;\;(B=BI_{p})$$ $\underline{Thm}$ Let $V,W$ be finite dimensional vector spaces with ordered bases $\beta, \gamma$ respectively. Let $T$ be linear. Then $$[T(u..

$\underline{Def}$ Let $A \in M_{n \times n}$. Define $A^{1}=A,\, A^{2}= A^{1} \cdot A.$ Define recursively that $A^{k}=A^{k-1} \cdot A$ $\forall \geq 2$. Define $A^{0}=I_{n}$. $\underline{Ex}$ $A=\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix},\; A^{2}=0$. Cancellation law does not hold for matrix product.

$\underline{Thm}$ Let $A \in M_{m \times n},\, B,C \in M_{n \times p},\, D,E \in M_{q \times m}$. Then $(a)$ $A(B+C)=AB+AC,\, (D+E)A=DA+EA$ $(b)$ $a(AB)=(aA)B=A(aB)$ $(a \in \mathbb{F})$ $(c)$ $I_{m}A=A=AI_{n}$ $(d)$ If $V$ is an n-dimensional vector space with an ordered basis, then $[I_{V}]_{\beta}=I_{n}$. $\underline{Proof \, of \, (c)}$ $$\displaystyle \begin{equation} \begin{split} (I_{m}A)..

www.backtrader.com/docu/ Introduction - Backtrader Introduction Welcome to the backtrader documentation! The platform has 2 main objectives: Ease of use Go back to 1 Note Loosely based on the Karate (Kid) rules by Mr. Miyagi. The basics of running this platform: Create a Strategy Decide on potential adjust www.backtrader.com 백테스팅 할 때 사용하는 모듈 github.com/sharebook-kr/pykrx sharebook-kr/pykrx KRX 주..

$\underline{Thm}$ Let $V,W,Z$ be vector spaces over $\mathbb{F}$, and let $T \colon V \rightarrow W$ & $U \colon W \rightarrow Z$ be linear. Then $UT=U \circ T \colon V \rightarrow Z$ is linear. $\underline{Thm}$ Let $V$ be a vector space. Let $T, U_{1}, U_{2} \in \mathcal{L}(V)=\mathcal{L}(V,V)$. Then $(a)$ $T(U_{1}+U_{2})=TU_{1}+TU_{2}, (U_{1}+U_{2})T=U_{1}T+U_{2}T$ $(b)$ $T(U_{1}U_{2})=(TU_{1..