벡터 자기회귀모델은 이전 포스팅에서 다루었던 자기회귀모델의 벡터꼴이다. 예시로 $VAR(1)$을 살펴보자.
$$\begin{bmatrix} r_{t} \\ q_{t} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} r_{t-1} \\ q_{t-1} \end{bmatrix} + \begin{bmatrix} \epsilon_{r,t} \\ \epsilon_{q,t} \end{bmatrix}$$
$$ \vec{x_{t}}=\textbf{A} \vec{x_{t-1}}+\vec{\epsilon_{t}}$$
이전 포스팅에서 $AR(1)=MA(\infty)$로 쓸 수 있던 것처럼 벡터꼴의 자기회귀모델 또한 $VAR(1)$을 $VMA(\infty)$로 쓸 수 있다. 이는 다음과 같다.
$$\begin{equation} \begin{split} & \;\;\;\;\;\, \vec{x_{t}}=\textbf{A}\vec{x_{t-1}}+\vec{\epsilon_{t}} \\ & \Rightarrow \vec{\epsilon_{t}}=\vec{x_{t}}+\textbf{A}\vec{x_{t-1}} \\ & \Rightarrow \vec{\epsilon_{t}}=\vec{x_{t}}-\textbf{A}L\vec{x_{t}} \\ & \Rightarrow \vec{\epsilon_{t}}=(\textbf{I}-\textbf{A}L)\vec{x_{t}} \\ & \Rightarrow \vec{x_{t}}=(\textbf{I}-\textbf{A}L)^{-1}\vec{\epsilon_{t}} \\ & \Rightarrow \vec{x_{t}}=(\textbf{I}+\textbf{A}L+\textbf{A}^{2}L^{2}+\cdots)\vec{\epsilon_{t}} \\ & \;\;\;\;\;\;\;\;\; = VMA(\infty) \end{split} \end{equation}$$
$VAR$을 사용하지, $VARMA$는 쓰지 않는다. $VARMA$는 추정하기 어렵기 때문인데, $VAR$ 모델의 경우에는 과거의 데이터만 필요하기 때문에 파라미터를 추정하는 데 있어 OLS(Ordianry Least Square)를 돌리면 된다. (MLE를 사용해도 되지만 OLS가 많은 경우 쉽고 편하다.) 하지만, $MA$ 모델은 인풋에 대한 에러텀을 요구하는데, 이는 관찰을 할 수 없기 때문에 OLS를 사용하는 것이 바람직하지 않다. 그래서 MLE를 사용하는데, 에러텀의 lag가 많아질수록 MLE 계산이 복잡해진다.
Converting Into VAR(1)
다행히, 우리는 모든 시계열을 $VAR(1)$로 변환해줄 수 있다. 이는 우리가 일반적으로 $VAR(1)$을 사용하는 이유가 된다.
우선 이 얘기를 하기 전, $ARMA(p,q)$ 모델을 먼저 정의하자.
$\underline{Def}$ (자기회귀-이동평균 모델)
$ARMA(p,q)=AR(p)+MA(q)$
$\underline{Ex}$
$ARMA(2,1)$을 생각해보자.
$$y_{t}=\phi_{1}y_{t-1}+\phi_{2}y_{t-2}+\epsilon_{t}+\theta_{1}\epsilon_{t-1}$$
이는 다음과 같이 바꿔 벡터꼴로 만들 수 있다.
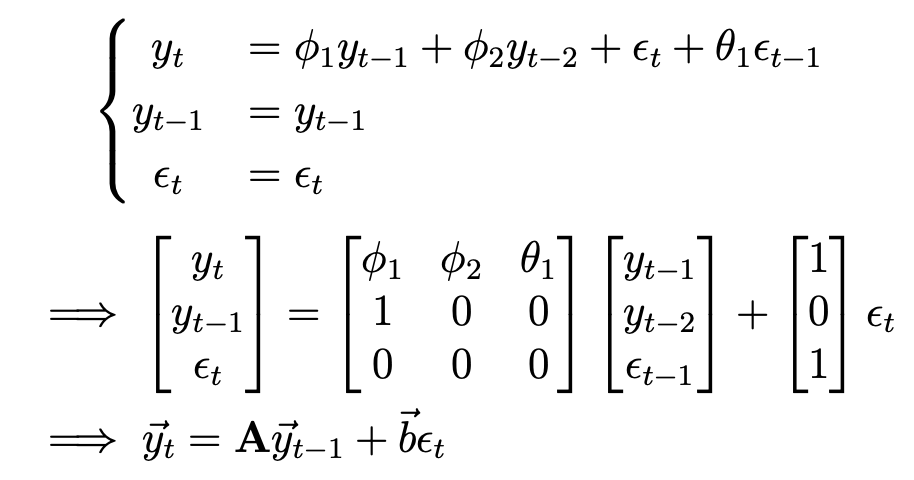
where $Var(\epsilon_{t})=\sigma_{\epsilon}^{2}\textbf{I}$
종종 shock의 variance matrix를 단위행렬이 되도록 쓰는 것이 편리한데, 위의 행렬식을 바꿔 써보자.

Forecasting
이제 $VAR(1)$ 모델을 이용하여 n-step forecasting을 해보자.
One Step Forecasting
$$\begin{equation} \begin{split} \mathbb{E}[\vec{x}_{t+1} \vert \vec{x_{t}}] & =\mathbb{E}[\textbf{A}\vec{x_{t}}+\vec{\epsilon_{t}} \vert \vec{x_{t}}] \\ & = \textbf{A} \vec{x_{t}} \end{split} \end{equation}$$
$$\begin{equation} \begin{split} Var[\vec{x}_{t+1} \vert \vec{x}_{t}] & = Var[\textbf{A}\vec{x}_{t} \vert \vec{\epsilon}_{t} \vert \vec{x}_{t}] \\ & = Var(\vec{\epsilon}_{t}) \end{split} \end{equation}$$
Two Step Forecasting
$$\begin{equation} \begin{split} \mathbb{E}[\vec{x}_{t+1} \vert \vec{x}_{t}] & = \mathbb{E}[\textbf{A}\vec{x}_{t+1}+\vec{\epsilon}_{t+1} \vert \vec{x}_{t}] \\ & = \mathbb{E}[\textbf{A}(\textbf{A}\vec{x}_{t}+\vec{\epsilon}_{t})+\vec{\epsilon}_{t+1} \vert \vec{x}_{t}] \\ & = \mathbb{E}[\textbf{A}^{2}\vec{x}_{t}+\textbf{A}\vec{\epsilon}_{t}+\vec{\epsilon}_{t+1} \vert \vec{x}_{t}] \\ & = \textbf{A}^{2} \vec{x}_{t} \end{split} \end{equation}$$
$$\begin{equation} \begin{split} Var[\vec{x}_{t+1} \vert \vec{x}_{t} & = Var[\textbf{A}^{2}\vec{x}_{t}+\textbf{A}\vec{\epsilon}_{t}+\vec{\epsilon}_{t+1} \vert \vec{x}_{t+1}] \\ & = Var[\textbf{A}\vec{\epsilon}_{t}+\vec{\epsilon}_{t+1} \vert \vec{x}_{t}] \\ & = \textbf{A}Var(\vec{\epsilon}_{t})\textbf{A}^{t}+Var(\vec{\epsilon}_{t}) \end{split} \end{equation}$$
n Step Forecasting
$$\mathbb{E}[\vec{x}_{t+n} \vert \vec{x}_{t}]=\textbf{A}^{n}\vec{x}_{t}$$
$$Var[\vec{x}_{t+n} \vert \vec{x}_{t}]=\textbf{A}^{n}Var(\vec{\epsilon}_{t})[\textbf{A}^{t}]^{n}+\cdots+\textbf{A}Var(\vec{\epsilon}_{t})\textbf{A}^{t}+Var(\vec{\epsilon}_{t})$$