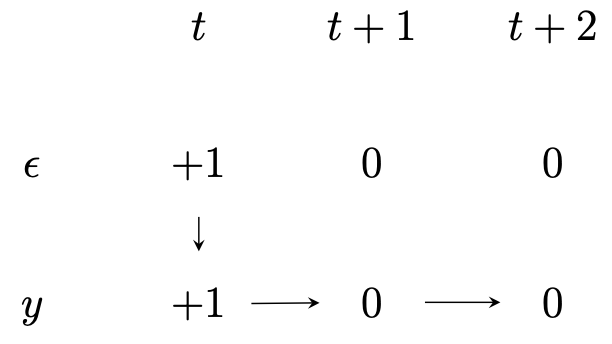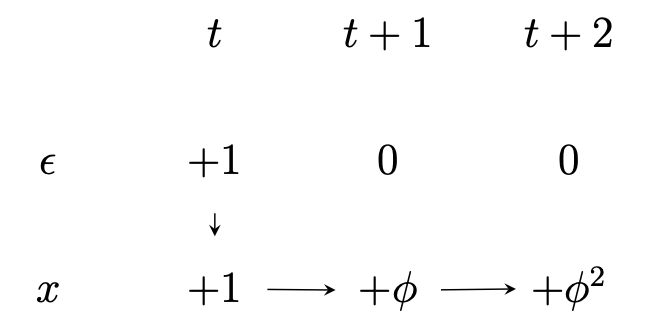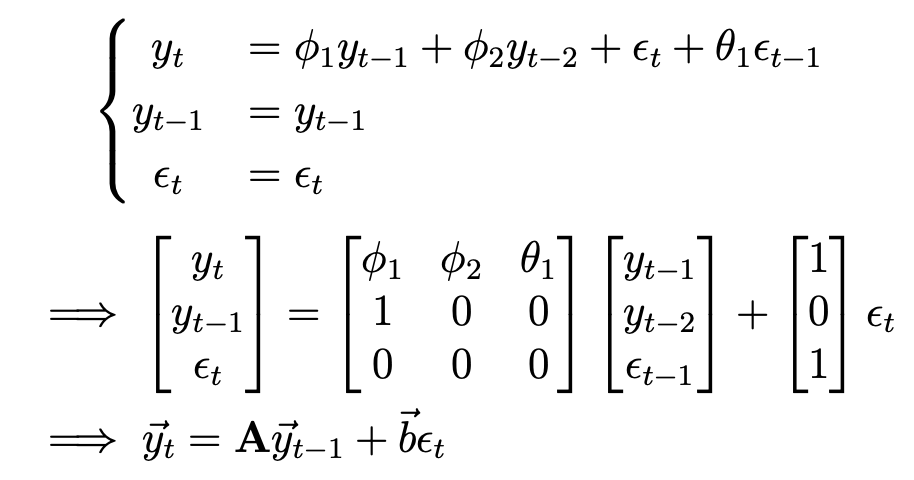Blog

일반적으로 적절한 변환을 거치면 time series process를 다음과 같이 쓸 수 있다. $$\phi (L) y_{t} = \theta (L) \epsilon_{t}\;\cdots\;(1)$$ 여기서 $\phi (L), \theta (L)$은 각각 다음과 같다. $$\phi (L) = 1 - \phi_{1}L-\phi_{2}L^{2}-\cdots-\phi_{p}L^{p}$$ $$\theta (L) = 1+\theta_{1}L+\theta_{2}L^{2}+\cdots+\theta_{q}L^{q}$$ 그러면 $\phi(L)$은 최대 p개의 근을, $\theta(L)$은 q개의 근을 갖는다. 이를 인수분해하면 다음과 같다. $$(1-\phi_{1}^{\ast}L)(1-\phi_{2}^{\ast}L)\c..

추세안정(Trend Stationary)과 랜덤워크(Random Walk)는 둘 다 유닛 루트를 갖는다. 하지만 얘들은 충격반응함수(Impulse Responsibiltiy Function)에서 다른 점이 드러난다. Trend Stationary 추세안정과정은 다음과 같다. $$y_{t}=\mu t + \theta (L) \epsilon_{t}$$ 여기서 추세를 빼면 다음과 같은 stationary process를 얻게 된다. $$y_{t}-\mu t = \theta (L) \epsilon_{t}$$ 여기다 양쪽에 일차 미분 $\nabla=(1-L)$을 양변에 적용해보면, $$\begin{equation} \begin{split} \nabla y_{t} & = \nabla \mu t + \nabla \t..

그레인저 인과성 검정(Granger Causality Test)은 시계열이 다른 걸 예측하는데도 유용한지 결정하는데 필요한 통계적 가설 검정이다. Ex1 다음과 같은 $VAR(1)$ model을 하나 생각해보자. $$\begin{bmatrix} r_{t} \\ q_{t} \end{bmatrix} = \begin{bmatrix} \mu_{r} \\ \mu_{q} \end{bmatrix} + \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} r_{t-1} \\ q_{t-1} \end{bmatrix} + \begin{bmatrix} \epsilon_{r,t} \\ \epsilon_{q,t} \end{bmatrix}$..

Variance Decomposition(or Forecast Error Variance Decomposition)은 자기회귀에서 각 변수가 다른 변수들에게 얼마나 영향을 끼치는지에 대한 정보의 양을 말한다. 이는 각 변수의 error variance가 얼마나 다른 변수에 대한 외생적 충격으로 설명될 수 있는지를 정한다. (외생적 충격 (exogeneous shock): 모델에서 생각안하는 쇼크) 이전 포스팅에서 $\vec{x}_{t}=\textbf{C}(L)\vec{\xi}_{t}, \, where \, Var(\vec{\xi}_{t})=\textbf{I}$를 정의했다. 그러므로, $$\begin{equation} \begin{split} \vec{x}_{t} & = \textbf{C}(L)\vec{\..

이전 포스팅에서는 두 변수를 코릴시키기 위해 'Cholesky Decompostion'을 배웠다. 우리의 최종 목적은 코릴돼있는 두 변수를 그렇지 않게 만드는 것이다. 우선, $\vec{x}_{t}=\textbf{C}(L)\vec{\xi}_{t}$를 다음과 같이 써보자. $$ \begin{bmatrix} y_{t} \\ z_{t} \end{bmatrix} = \begin{bmatrix} C_{0,yy} & C_{0,yz} \\ C_{0,zy} & C_{0,zz} \end{bmatrix} \begin{bmatrix} \xi_{y,t} \\ \xi_{z,t} \end{bmatrix}+\textbf{C}_{1}\vec{xi}_{t-1}+\cdots$$ Sims는 $\textbf{C}_{0}$가 lower-tr..

Cholesky Decomposition Cholesky Decomposition은 두 변수를 코릴시키려고 쓴다. 예를 들어서, 두변수 $y, z$가 공분산 행렬(covriance matrix) $\textbf{I}$를 갖는다 쳐보자. 그리고 $y, z$가 공분산 $\rho$를 갖게 다른 변수로 변환을 시켜주고 싶다. 아이디어는 간단하다. 우리가 random vector $\vec{x}=\begin{bmatrix} y \\ z \end{bmatrix}$를 계산할 때, 이를 다음과 같이 계산한다. $$\begin{equation}\begin{split} Var(\textbf{A}\vec{x}) & = \textbf{A}Var(\vec{x})\textbf{A}^{t} \\ & = \textbf{A}\text..

주어진 시계열에 대해서 쇼크가 났다고 쳐보자. 그럼 이후의 시계열에 대해 쇼크의 behaviour에 대해 이것이 지속적인 것인지, 일시적인 것인지 궁금할 것이다. 이를 분석하기 위해 $VAR$ model을사용할 수도 있다. 먼저 $AR(1)$을 살펴보자. $$x_{t}=\phi x_{t-1}+\epsilon_{t}$$ 쇼크를 준다는 건 노이즈$\epsilon_{t}$에 어떤 값을 넣는 것이다. $\epsilon_{t}$에 1을 넣어보자. $$x_{t}=\phi x_{t-1}+1$$ $$x_{t+1}=\phi x_{t}+\epsilon_{t+1}$$ 이제 $x_{t+1}$식에 $x_{t}$에 쇼크를 대입한 값을 넣어 정리해보자. $$\begin{equation} \begin{split} x_{t+1} & ..

벡터 자기회귀모델은 이전 포스팅에서 다루었던 자기회귀모델의 벡터꼴이다. 예시로 $VAR(1)$을 살펴보자. $$\begin{bmatrix} r_{t} \\ q_{t} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} r_{t-1} \\ q_{t-1} \end{bmatrix} + \begin{bmatrix} \epsilon_{r,t} \\ \epsilon_{q,t} \end{bmatrix}$$ $$ \vec{x_{t}}=\textbf{A} \vec{x_{t-1}}+\vec{\epsilon_{t}}$$ 이전 포스팅에서 $AR(1)=MA(\infty)$로 쓸 수 있던 것처럼 벡터꼴의 자기회귀모델 또한 $VAR(1)$을 $V..

$\underline{Def}$ (Auto-Regressive $p$ Model, AR Model) 자기회귀 p모델 $x_{t}$은 다음과 같이 정의된다. $$x_{t}=\phi_{1}x_{t-1}+\phi_{2}x_{t-2}+\cdots+\phi_{p}x_{t-p}+\epsilon_{t} \;\; where\, \vert \phi \vert < 1$$ 여기서 $\phi$는 모델의 파라미터를, $\epsilon_{t}$는 노이즈를 뜻한다. $\underline{Def}$ (Lag-Operator) 여기서 다음 성질은 갖는 lag-operator $L$을 정의하자. 이는 시계열에서 이전 값을 내놓는 함수다. $(1)$ $L \phi = \phi$ $(2)$ $Lx_{t}=x_{t-1}$ $(3)$ $L^{..