주어진 시계열에 대해서 쇼크가 났다고 쳐보자. 그럼 이후의 시계열에 대해 쇼크의 behaviour에 대해 이것이 지속적인 것인지, 일시적인 것인지 궁금할 것이다. 이를 분석하기 위해 $VAR$ model을사용할 수도 있다. 먼저 $AR(1)$을 살펴보자.
$$x_{t}=\phi x_{t-1}+\epsilon_{t}$$
쇼크를 준다는 건 노이즈$\epsilon_{t}$에 어떤 값을 넣는 것이다. $\epsilon_{t}$에 1을 넣어보자.
$$x_{t}=\phi x_{t-1}+1$$
$$x_{t+1}=\phi x_{t}+\epsilon_{t+1}$$
이제 $x_{t+1}$식에 $x_{t}$에 쇼크를 대입한 값을 넣어 정리해보자.
$$\begin{equation} \begin{split} x_{t+1} & =\phi x_{t}+\epsilon_{t+1} \\ & = \phi(\phi x_{t-1}+1)+ \epsilon_{t+1} \end{split} \end{equation}$$
이를 $x_{t+2}$에도 똑같이 대입하여 정리해보자.
$$\begin{equation} \begin{split} x_{t+2} & = \phi x_{t+1}+\epsilon_{t+2} \\ & = \phi[\phi(\phi x_{t-1}+1)+\epsilon_{t+1}]+\epsilon_{t+2} \end{split} \end{equation}$$
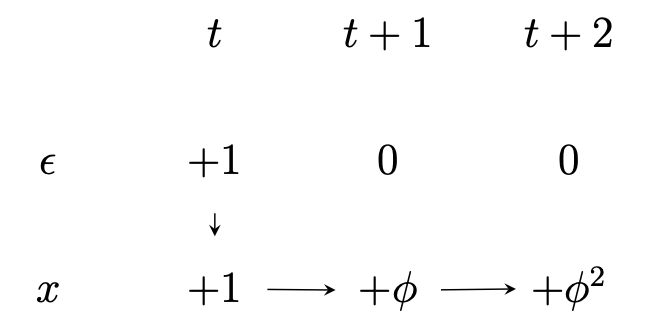
1을 넣었기 때문에 쇼크가 영속적이라는 것을 확인할 수 있다. $t=1$일 때 프로세스는 $+1$을 갖는다. $t=2$일 때는 $+\phi$를 갖고, $t=n$일 때는 $+\phi^{n}$을 갖는다. 여기서 $\vert \phi \vert < 1$이기 때문에 시간이 무한이 지난다면 이는 사라질 것이다. 그래서 충격반응그래프(Impulse Responsibility Graph)는 다음과 같이 그려진다.

그럼 $AR(1)$이 아니라 $VAR(1)$인 경우에는 어떻게 될까?
$$\vec{x}_{t}=\begin{bmatrix} y_{t} \\ z_{t} \end{bmatrix} = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix} \begin{bmatrix} y_{t-1} \\ z_{t-1} \end{bmatrix} + \begin{bmatrix} \epsilon_{t,y} \\ \epsilon_{z,t} \end{bmatrix}$$
여기서 $\epsilon_{y,t}$에 쇼크를 줬다고 해보자.

$x,y$는 과거의 아웃풋을 공유하기 때문에 변수가 한가지일 때보다 복잡하다. ($y_{t}$의 식을 보면 $z_{t-1}$이, $z_{t}$를 보면 $y_{t-1}$이 있는 걸 보면 알 수 있다.) 이는 변수가 더 많아지거나 시계열이 많은 lags를 요구한다면 더 상황이 안좋아진다. 그래서 이를 일반화하는 시도가 필요하다. 먼저 첫번째 포스팅에서 다루었던 lag operator를 고려해보자.

이게 univariate case라면 $[\textbf{I}-\phi L]\vec{x}_{t}=\vec{\epsilon}_{t}$에서 계수는 유닛 쇼크에 대한 정보를 준다. 그래서 우리는 계수 $\phi, \phi^{2}, \cdots$를 충격반응함수(Impulse Responsibility Function)이라고 부른다. 또한 행렬 $\phi$의 각 원소는 현재와 과거 변수들의 관계를 알려준다. 예를 들어
$$\begin{equation} \begin{split} \phi & = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix} \\ & = \begin{bmatrix} y_{t-1} \rightarrow y_{t} & z_{t-1} \rightarrow y_{t} \\ y_{t-1} \rightarrow z_{t} & z_{t-1} \rightarrow z_{t} \end{bmatrix} \end{split} \end{equation}$$
라고 한다면, $\phi_{11}$은 $y_{t},y_{t-1}$간의 관계를 $\phi_{12}$는 $y_{t},z_{t-1}$간의 관계를 알려준다. 우리가 시계열을 $\vec{x}_{t+1}=\phi \vec{x}_{t}+\vec{\epsilon}_{t}$로 정의한다면,
$$\begin{equation} \begin{split} \phi & = \begin{bmatrix} y_{t} \rightarrow y_{t+1} & z_{t} \rightarrow y_{t+1} \\ y_{t} \rightarrow z_{t+1} & z_{t} \rightarrow z_{t+1} \end{bmatrix} \\ & = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix} \end{split} \end{equation}$$
이 된다. $\epsilon_{t}$ 앞에 계수가 없고 유닛 쇼크를 줬기 때문에 $\epsilon_{y,t}=1$로 하거나 $\epsilon_{z,t}=1$로 한다면 $y_{t}$나 $z_{t}$는 1씩 증가할 것이다. 그래서 $\phi$에 대한 표현은 실제로 다음과 같다.
$$\begin{equation} \begin{split} \phi & = \begin{bmatrix} \epsilon_{y,t} \rightarrow y_{t+1} & \epsilon_{z,t} \rightarrow y_{t+1} \\ \epsilon_{y,t} \rightarrow z_{t+1} & \epsilon_{z,t} \rightarrow z_{t+1} \end{bmatrix} \\ & = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix} \end{split} \end{equation}$$
그러므로,
$$\begin{equation} \begin{split} \phi^{2} & = \begin{bmatrix} \epsilon_{y,t} \rightarrow y_{t+2} & \epsilon_{z,t} \rightarrow y_{t+2} \\ \epsilon_{y,t} \rightarrow z_{t+2} & \epsilon_{z,t} \rightarrow z_{t+2} \end{bmatrix} \\ & = \begin{bmatrix} \phi_{11}^{2}+\phi_{12}\phi_{21} & \phi_{11}\phi_{12}+\phi_{12}\phi_{22} \\ \phi_{21}\phi_{11}+\phi_{22}\phi_{21} & \phi_{21}\phi_{12}+\phi_{22}^{2} \end{bmatrix} \end{split} \end{equation} $$
이를 $k$번 한다 생각해보면,
$$\phi^{k}=\begin{bmatrix} \epsilon_{y,t} \rightarrow y_{t+k} & \epsilon_{z,t} \rightarrow y_{t+k} \\ \epsilon_{y,t} \rightarrow z_{t+k} & \epsilon_{z,t} \rightarrow z_{t+k} \end{bmatrix}$$
이들이 correlated돼있는 경우라면 어떻게 할까? 만약 얘네들이 서로 상관돼있으면 첫번째 쇼크가 온 이후에 또다른 쇼크도 올 것이다. 이 경우에는 계산이 더 어려워질 수 있는데 두 가지 과정을 지나면 쉽게 계산할 수 있다.
1. 변수간 상관관계를 없애기 위해 변수 변환을 해준다.
2. 충격반응함수(Impulse Responsibility Function)을 계산한다.
변수간 상관관계를 없애주기 위해서는 'Cholesky Decomposition'을 알아야 한다. 이는 다음 포스팅에서 다루겠다.