멀티코어 프로세서를 다루며 Memory Hierarchy Design은 우리에게 더 중요해졌습니다. 프로그램을 짜는 입장에서는 메모리 걱정없이 작업을 하는 게 가장 이상적일텐데, 그러려면 이상적인 메모리가 필요하겠죠. 그러면 어떤 메모리가 이상적인 메모리일까요? 이상적인 메모리는 다음과 같은 특징을 가진 메모리입니다.
Ideal Memory
- Zero access latency
- Infinite bandwidth
- Infinite capacity
- Zero cost
하지만 이런 특징은 서로 상충합니다.
- 메모리가 크면 읽거나 쓸 때 긴 시간이 걸릴 것이고
- 빠르고 큰 대역폭을 가진 메모리는 비쌉니다. (SRAM vs DRAM vs Disk vs Tape)
SRAM은 리프레쉬가 필요없고 capacitor가 아니기 때문에 빠르지만 집약도가 낮고 비쌉니다. 반면에 DRAM은 리프레쉬가 필요하고 capacitor이기 때문에 느립니다. 그렇지만 집약도가 높고 쌉니다. 디스크들 중에 HDD와 SSD를 비교해도 똑같습니다. 살펴봤듯이 이상적인 메모리를 디자인하는 것은 불가능해보입니다. 그러면 이 문제를 어떻게 해결할 수 있을까요?
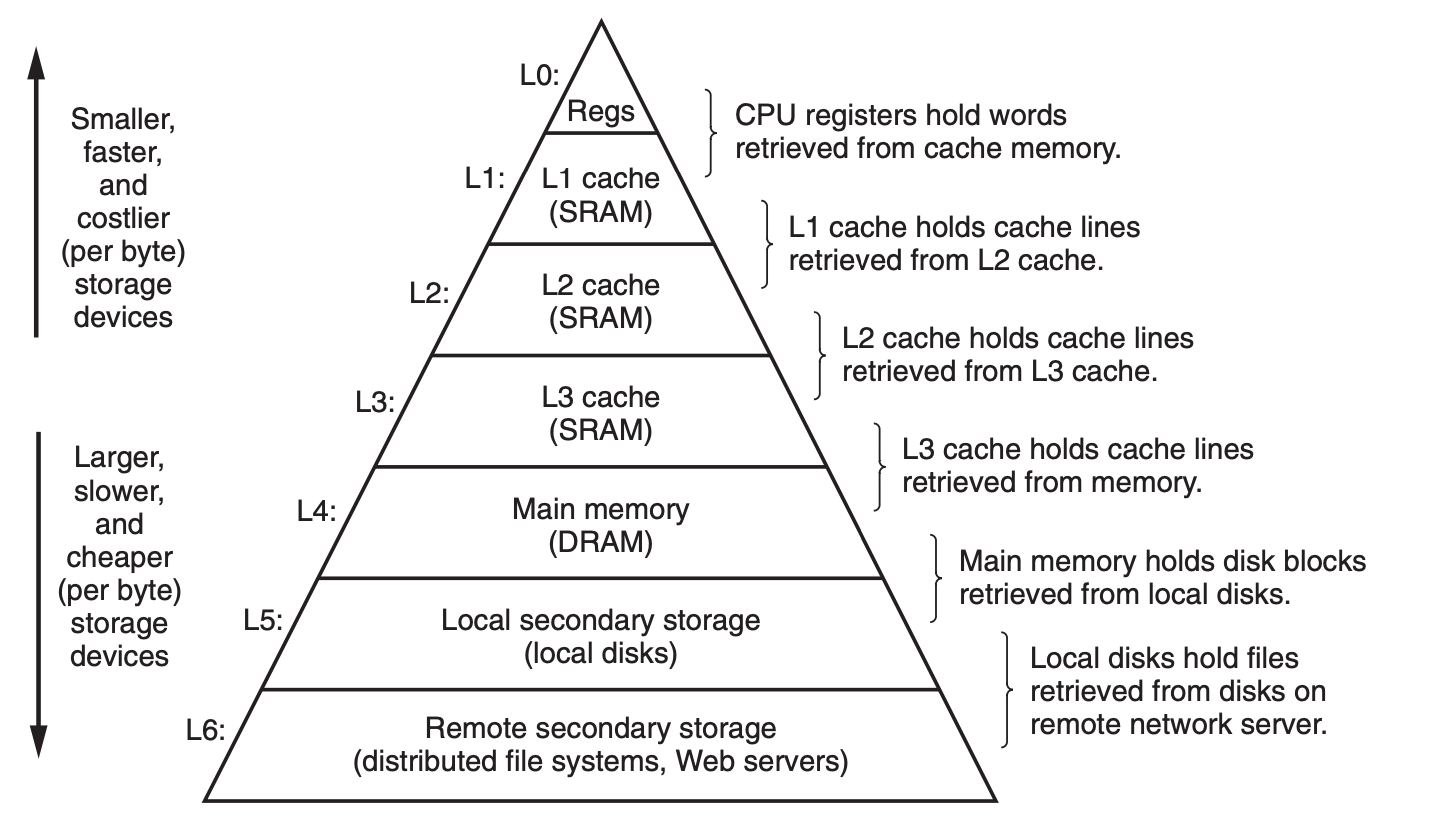
이에 대한 답은 'Memory Hierarchy'입니다. 이건 서로 다른 속도와 크기를 가진 메모리를 여러 계층으로 쌓는 걸 말합니다. 그러면 메모리는 계층에서 가장 큰 것처럼 느껴지지만 속도는 가장 빠른 계층의 것을 쓰는 것처럼 느낄 수 있습니다. 이때 계층이 높아질수록 메모리의 사이즈는 점점 작아지고 빠르게 설계를 합니다. 여기까지 이야기하면 괜히 약파는 것 같은데, 되는 이유가 있으니까 배우겠죠? Locality가 이를 보장해줍니다. Locality라는 건 메모리의 사용됐던 영역이 다음에도 사용되는 것을 이야기합니다.
Locality에는 'Temporal Locality'와 'Spatial Locality' 두가지가 있습니다. Temporal locality는 데이터가 최근에 접근했던 영역을 다시 접근할 확률이 높은 성질을 이야기합니다. 루프문을 생각해보면 됩니다. Spatial locality는 데이터가 최근에 접근했던 영역의 인근을 접근할 확률이 높은 성질을 이야기합니다. 어레이 데이터를 생각해보면 됩니다. 우리가 코드를 짤 때는 루프문이나 어레이를 거의 항상 사용하는데 이런 걸 exploit할 것입니다.
이렇게 Memory Hierarchy를 이야기했고, 이게 왜 잘 되는지, 잘 될 것인지 이야기했습니다. 그런데 데이터가 메모리들을 옮겨다니며 항상 최적으로 작동할까요? 현실적으로 그렇지 않을 것입니다. 이를 자세히 이야기하기 위해 'Block', 'Hit', 'Miss'라는 개념을 정의하겠습니다.
Blcok
: 캐시 메모리에서 스토리지의, 정보의 기본 단위입니다. Memory Hierarchy에서 각 메모리들은 정보를 주고받기 위해 블록을 주고받습니다.
Hit
: CPU에서 요청한 블록이 캐시 메모리에 있는 경우를 이야기합니다. 혹은 하위 계층의 메모리에서 요청한 블록이 상위 계층에 존재는 경우를 이야기합니다. 이때 Hit rate은 다음과 같습니다. Hit rate = hits/accesses
Miss
: CPU에서 요청한 블록이 캐시 메모리에 없는 경우를 이야기합니다. 혹은 하위 계층의 메모리에서 요청한 블록이 상위 계층에 없는 경우를 이야기합니다. Hit와 정반대데, Miss rate은 다음과 같습니다. Miss rate = 1 - hit rate
'컴퓨터 > 컴퓨터구조특론' 카테고리의 다른 글
| [ACA] Improving Cache Performance (0) | 2020.04.13 |
|---|---|
| [ACA] Memory Hierarchy and Caches (4) (0) | 2020.04.12 |
| [ACA] Memory Hierarchy and Caches (3) (1) | 2020.04.12 |
| [ACA] Memory Hierarchy and Caches (2) (0) | 2020.04.10 |
| Fundamentals (0) | 2020.04.05 |