Paper Link: https://arxiv.org/abs/1607.04381
Github: x
Introduction
ICLR 2017에 게재된 논문입니다. 이 논문에서는 pre-trained network를 pruning을 통해 sparse하게 만든 뒤 re-dense하게 만들었더니 성능이 향상됐음을 보이는 실험적인 논문입니다. 저자가 Song.Han이라는 분으로 이전의 리뷰한 논문의 연장선상에 있다고 볼 수 있는데요. 당시에 pruning을 60%가량 했음에도 불구하고 약간의 accuracy 향상이 있다는 것에 착안하여 pruning을 통해서 feature extraction을 잘 해주는 weight들을 골라냈으니 이걸 갖고서 training을 하면 더 나은 accuracy 향상을 보일 수 있지 않을까? 생각으로 진행된 연구입니다.
DSD Training Flow
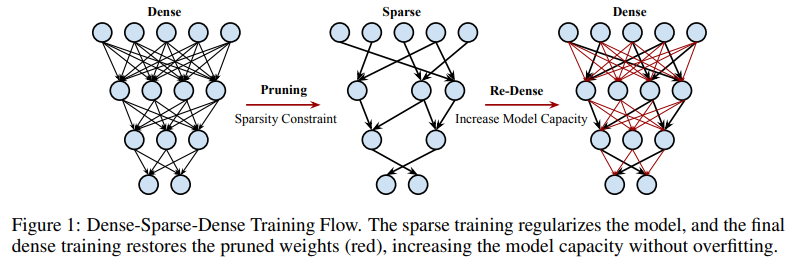
첫 dense phase의 경우에는 gradient descent를 이용하여 network를 학습하였습니다. 일반적으로 neural network를 학습시키는 과정과 똑같습니다. 이제 sparse phase가 중요한데요. 여기서는 위에서 언급한 방법을 그대로 사용하여 threshold기반으로 abs value가 작은 weight들을 pruning하였습니다. 그런데 다른 점이라면 왜 적은 weight을 pruning하였냐에 대해서 설명을 해두었습니다. 이는 다음과 같습니다.
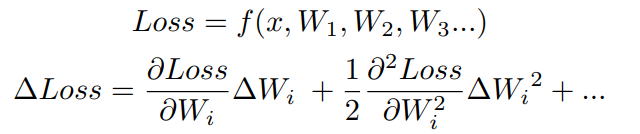
위의 식은 우리가 gradient descent로 optimize할 loss function과 이의 taylor expansion입니다. 여기서 하고 싶은 게 loss를 최소화하는 방향으로 weight을 thresholding을 하는 건데 이걸 하려면 taylor expansion에서 dominant한 항인 첫 번째와 두 번째 항을 최소화 시켜줘야 합니다. 그런데 pruning을 하면 parameter가 0이 되기 때문에 첫 번째 항은 실질적으로 0이 되어서 두 번째 항이 중요하게 됩니다. 그런데 이걸 계산하려면 loss의 hessian matrix를 계산해줘야 되는데, 이때 time complexity가 O(n^2)라 computation cost가 너무 높습니다. 그래서 이에 대한 차선으로 abs value가 작은 weight을 pruning해줍니다. (loss function의 taylor expansion을 통해서 어떤 weight을 pruning하는지 정하는 최초의 논문은 Yahn Lecun의 "Optimal Brain Damage"라는 논문입니다.)
그리고 여기서 pruning을 할 때는 각 layer W에 대해 N개의 weight들을 sorting하고, N * (1 - sparsity) 번째 weight을 threshold로 잡아서 이것보다 작은 weight을 pruning해주는 binary mask를 만들어 줍니다. Training을 할 때는 남은 weight들에 대해서만 update를 해주었고, 각 layer에 대해서 모두 동일한 sparsity를 적용해 pruning을 해주었습니다.
마지막 dense phase에서는 pruned weight들을 0으로 re-initialize시켜주고 난 뒤 training시켜줬습니다. 여기서 learning rate는 맨 처음 dense phase의 network의 1/10으로 잡았는데, 논문에서는 sparse network가 수렴해서 좋은 local minima에서 시작하기 때문에 이를 작게 잡아도 괜찮다고 설명하고 있습니다. 그리고 dropout ratio나 weight decay같은 다른 hyperparameter는 동일하게 설정해두었습니다.
이에 대한 알고리즘과 weight distribution은 다음과 같습니다.

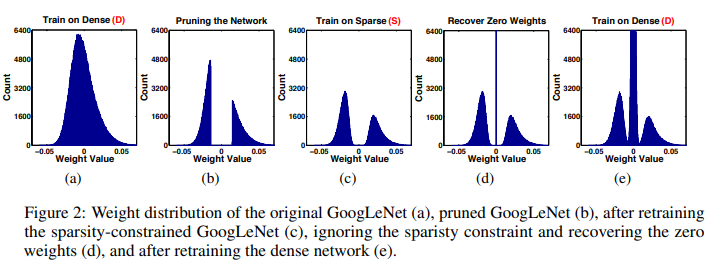
Experiments
본 논문에서는 vision, captioning, speech와 같은 다양한 도메인에 대해서 DSD가 적용 가능함을 보여주었습니다. 이는 다음과 같습니다.

Discussion
개인적으로는 왜 DSD가 퍼포먼스를 향상시킬까에 대해서 궁금했는데, 본 논문에서는 이 파트에서 몇가지 이유를 제시하며 왜 잘되는지에 대한 썰을 풀어 두었습니다.
- Escape Saddle Point
- Significantly Better Minima
- Regularized and Sparse Training
- Robust re-initialization
- Break Symmetry
놀라운 결과지만 어떻게, 왜 높은 퍼포먼스를 보이는 지에 대해서는 와닿는 설명이 없어 한편으로는 조금 찝찝한 마음이 있습니다... ㅎㅎ