Introduction
본 논문은 기존 경량화 모델에서 고려됐던 metric인 FLOPs이 간접적인 메트릭임을 지적하며 직접적인 메트릭인 speed와 latency를 언급했다. 더불어 네트워크 디자인에 대한 가이드라인을 제시하며 이에 따라 업그레이드된 ShuffleNetV2를 제안한다.
기존의 경량화 모델들은 주로 depth conv, ptwise conv, group conv과 같은 tensor decomposition을 활용하여 FLOPs을 줄이는 걸 목표로 디자인했다. 이를 따르면 실제 기기에 올라갈 때 빨라질 것 같지만 그렇지 않다. FLOPs만을 고려하는 디자인은 sub-optimal한 디자인일 수 밖에 없다.
1) FLOPs에는 영향을 덜 끼치지만 speed에는 영향을 끼치는 팩터가 있기 때문이다. FLOPs을 줄이더라도 memory access cost(MAC)가 높고 degree of parallelism이 낮다면 해당 모델은 느릴 것이다.
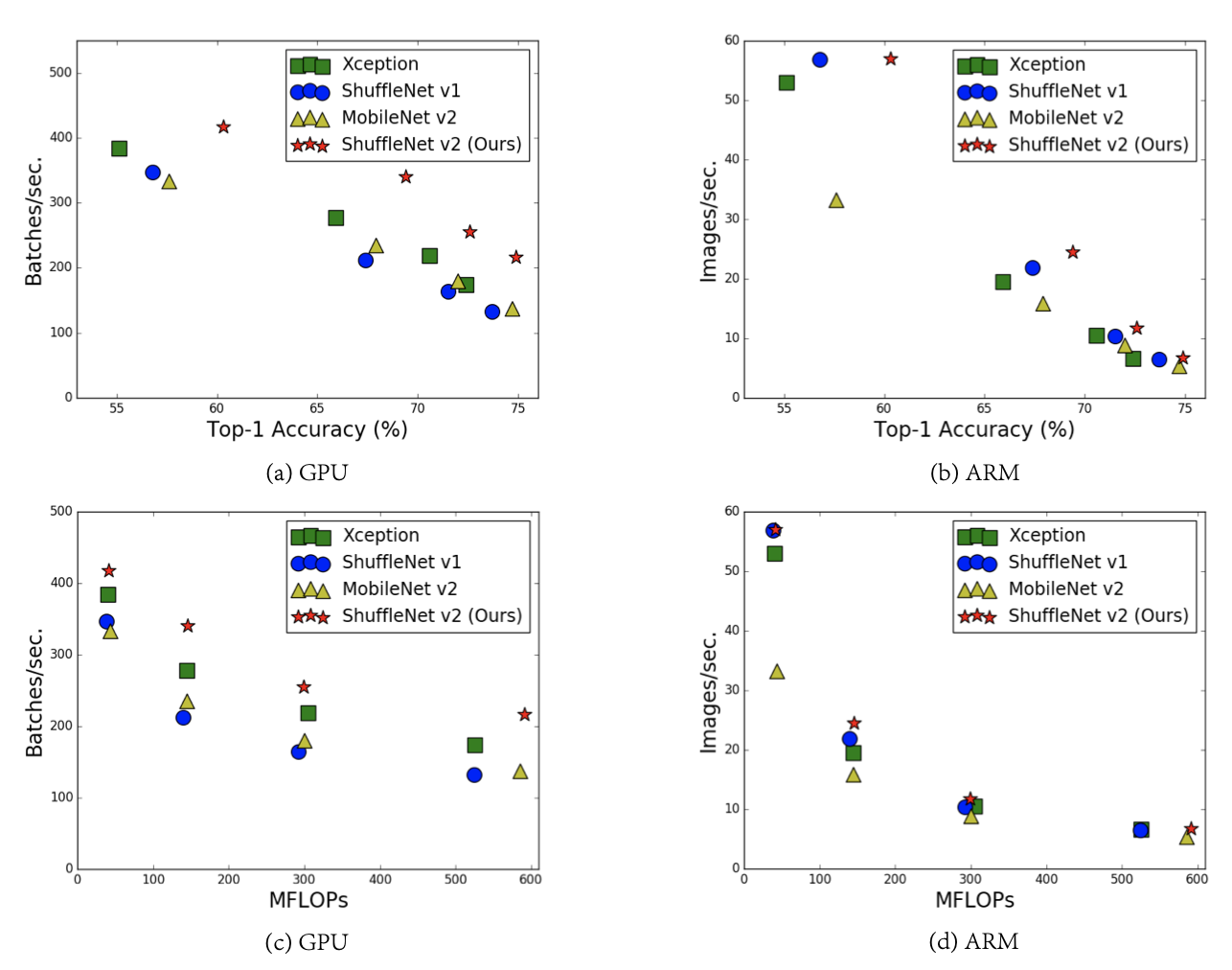
2) 어떤 하드웨어 플랫폼에서 돌리냐에 따라 같은 FLOPs을 갖더라도 다른 실행시간을 가질 수 있다. 위에서 언급한 tensor decomposition은 약간의 정보 손실은 감수하더라도 행렬 곱셈을 가속하기 위해 사용되는 기법이지만 GPU와 같은 높은 병렬성을 갖는 플랫폼에서는 FLOPs을 75%가량 줄여도 느려진다. 이는 당시 cudnn 라이브러리가 1x1 conv에는 최적화돼있지 않고 3x3 conv에만 최적화됐기 때문이다. (이때 사용된 것은 cudnn 7.0이다.)
피규어의 (c), (d)를 보면 이를 프랙티컬하게 확인할 수 있다.
이에 따라 효율적인 네트워크 디자인을 위한 네 가지 가이드라인을 제시한다.
Practical Guidelines for Efficient Network Design
G1) Equal channel width minimizes memory access cost (MAC)

당시 Xception, MobileNet과 같은 네트워크의 경우 depthwise seperable conv를 사용했는데, 이때 1x1 conv가 전체 연산량에 많은 비율을 차지했다는 것은 이전 리뷰에서 살펴봤다. 여기서 1x1 conv의 kernel shape에 따라 속도에 어떤 영향을 끼치는 지 알아보겠다. 커널의 크기는 정해져있으니 인풋/아웃풋 채널 개수만 정하면 된다. 이를 각각 $c_1, c_2$라고 하자. 피쳐맵의 크기를 $hw$라고하면 1x1 conv의 FLOPs은 $B=hwc_1 c_2$가 된다. 그러면 input/output feature map을 읽고 쓰는 데 $hw(c_1+c_2)$가 들고 커널의 가중치를 가져오는데 $c_1 c_2$만큼 들어 코스트는 다음과 같이 계산된다.
$MAC=hw(c_1+c_2)+c_1 c_2$
산술기하평균을 이용해 하한을 계산하면 다음과 같다.
$\displaystyle MAC\geq 2\sqrt{hwB}+\frac{B}{hw}$
그럼 $MAC$이 하한이 되려면 어떻게 해야될까? 인풋/아웃풋 채널의 개수를 같게 만들어주면 된다. 위의 표는 인풋/아웃풋 채널 개수 비에 따라 GPU, ARM위에서 성능을 나타내는 것이다. 채널 개수가 같은 경우 모든 하드웨어에서 가장 빠르고 차가 커질수록 점점 느려지는 것을 프랙티컬하게 확인할 수 있다.
G2) Excessive group convolution increases MAC

Group conv를 하면 $MAC$을 키운다는 이야기다. 위에서 계산한 공식을 ShuffleNet에 사용된 1x1 group conv에 적용하면 다음과 같다.
$\displaystyle MAC=hw(c_1+c_2)+\frac{c_1 c_2}{g}$
Group conv를 수행했기 때문에 연산량 또한 그룹의 크기만큼 줄어들어 $\displaystyle B=\frac{hwc_1 c_2}{g}$가 된다. 이때 인풋 $c_1 \times h \times w$와 연산량 $B$가 고정됐다 가정하고 위의 식을 고치면 다음과 같다.
$\displaystyle MAC=hwc_1+\frac{Bg}{c_1}+\frac{B}{hw}$
식에서 확인할 수 있듯이 그룹의 크기를 키우는만큼 $MAC$이 늘어나는 것을 이론적으로 알 수 있다. 위의 표는 그룹의 크기에 따라 GPU와 CPU에서의 속도를 나타낸 것이다. 그룹을 키울수록 모든 하드웨어에서 속도가 느려짐을 프랙티컬하게 확인할 수 있다.
이전 포스팅에서 ShuffleNet에서는 그룹의 크기를 키울수록 성능이 올라가는 것을 확인했다. 하지만 그룹의 크기를 키우면 $MAC$이 커져 속도가 느려지므로 성능과 속도간 트레이드 오프가 있는 것을 알 수 있다. 그러므로 그룹의 크기를 정할 때는 신중하게 선택해야 할 것이다.
G3) Network fragmentation reduces degree of parallelism

구글넷 시리즈에 사용된 Inception module은 모듈 내에 다양한 크기의 커널을 여러 개 갖고 있었다. ResNet은 블록 내에 2-3개의 커널을 갖고 있고, NASNET-A는 13개의 커널을 갖고 있다. (여기서는 이렇게 쪼개진 커널들을 'fragmented operators'라고 부른다. 이는 다양한 receptive field를 반영할 수 있기 때문에 정확도 측면에서는 장점을 갖고 있지만 GPU같은 병렬성이 높은 하드웨어에서는 커널 런칭이나 동기화같은 이슈때문에 속도가 느려진다.

위의 표는 fragment operator의 개수에 따라, 그리고 이를 순차적으로 두었는지, 병렬적으로 두었는지에 따라 GPU, CPU상에서 속도를 나타낸 것이다. Fragement operator를 늘릴수록 CPU에서는 성능차의 최대가 약 10%지만 GPU에서는 약 4배 가량 떨어지는 것을 확인할 수 있다. 그리고 이를 늘릴수록 모든 하드웨어에서 속도가 느려지는 것을 프랙티컬하게 확인할 수 있다.
G4) Element-wise operations are non-negligible

위의 표는 GPU, ARM에서 셔플넷과 모바일넷의 런타임을 나타낸 표다. 보통 element-wise operation이라고 하면 ReLU, AddTensor, AddBias와 같은 것을 말하는데, 이는 FLOPs이 낮기 때문에 디자인을 할 때 중요하게 여겨지지 않는다. 하지만 위에서 확인할 수 있듯이 GPU에서는 15-23%정도 런타임을 잡아먹는 걸 알 수 있다. 이는 적은 FLOPs을 갖고 있지만 MAC이 상당히 크기 때문이다.

이를 검증하기 위해 ResNet에서 사용됐던 1x1 conv -> 3x3 conv > 1x1 conv, shortcut path에 대해 실험했다. ReLU, shortcut path 사용 유무로 이를 나타냈다. GPU, CPU 모두 ReLU나 shortcut을 사용하지 않는 경우에 일관적인 성능 향상을 보였고, 이를 모두 사용하지 않을 때는 약 20% 성능 향상이 있는 걸 프랙티컬하게 확인할 수 있다.
ShuffleNet V2: an Efficient Architecture

왼쪽의 (a), (b)는 기존의 셔플넷 유닛을 나타내는 것이다. 기존 유닛은 ptwise group conv와 bottleneck structure를 썼기 때문에 G1, G2를 따르지 않아 $MAC$을 증가시킬 것이다. 그리고 group conv시에 그룹의 크기를 많이 키운다면 이는 G2, G3를 따르지 않는 것과 유사할 것이고 (a)에 있는 Add는 G4에 어긋난다. 이제 중요해지는 것은 dense conv나 group conv를 사용하지 않으면서 어떻게 인풋/아웃풋 채널 개수는 유지하며, 개수를 늘릴 수 있을 지가 된다.
Channel Split and ShuffleNet V2
- ShuffleNetV2는 채널 스플릿을 통해 인풋 채널을 두 개로 나눴다.
- fragmentation operate를 하지 않기 위해 브랜치 하나는 identity mapping으로 두었다. (G3)
- 다른 브랜치에서는 인풋/아웃풋 채널 개수를 갖게끔 세개의 conv를 두었다. (G1)
- 따라 모든 1x1 conv는 group conv를 사용하지 않았다. 처음에 채널 스플릿을 했기 때문에 부분적으로 따랐다. (G2)
- conv이후에는 channel concat을 하였다. 총 채널 개수는 같게 유지됐다.
- concat이후에는 channel shuffle을 진행했다.
- 마지막에 concat, channel shuffle을 하고 다음 shuffle unit으로 넘어가는 부분에서 channel split을 하는데 이 세개를 하나의 element-wise operation으로 합쳤다. (G4)
Analysis of Network Accuracy
ShuffleNetV2는 좋은 성능 성능을 보이는 데 크게 두 가지 이유를 꼽았다.
1) 각 블록의 높은 효율성이 더 많은 피쳐 채널을 사용하게끔 하여 모델의 캐퍼시티를 높였다.
2) 각 블록에서 인풋 피쳐 채널의 절반이 다음 블록으로 direct하게 가기 때문에 feature reuse가 생긴다. (DenseNet, CondenseNet)
Experiment

